LogD

Overview

This module calculates the logarithm of the apparent octanol-water partition coefficient D for all (including ionized) compound species at various pH values. Prediction results are presented in two ways – an easy to navigate and interpret graph and a list of LogD predictions at discrete pH values. Initially this list is populated by the LogD predictions at physiologically relevant pH conditions; however it is fully customizable via the ability to add or remove the predictions at any pH value.

Interface

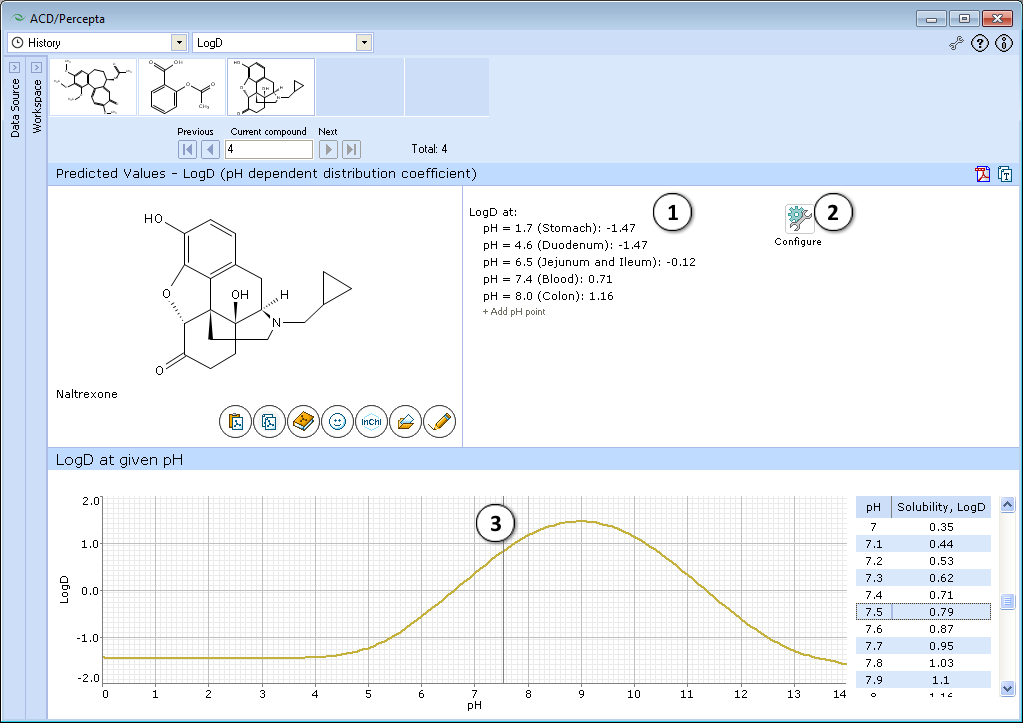
1. Displays several logD values at physiologically relevant pHs.
   
   
   
   a. Click "+/-" nodes to expand/collapse the option of new pH point's addition.
   b. Enter desirable pH value and press "Add". The new pH point along with automatically calculated logD value will appear at the end of the list.
   c. Hover over the pH point and press the "x" pictogram to remove it from the list.


2. Press "Configure" button to select LogP and pKa calculation algorithms, and libraries to use for training, or set other options.
   
   NOTE: Training takes place through LogP Self-training Libraries. The training procedure implemented in ACD/LogP GALAS module accepts LogD values measured at any pH and automatically recalculates these to the respective LogP of neutral species to be stored in the library. The trained LogP library may then be used in both LogP and LogD calculations.


3. Click and drag the slider to see calculated logD at precise pH value displayed on the right.

Technical information

Introduction to the Dissociative Partition Coefficient

Hydrophobicity is a very important physicochemical property used in different areas of chemistry, medicine and pharmacology. It is a very important indicator of transport and permeation through membranes, interaction with biological receptors and enzymes, toxicity, and biological potency [1,2]. In environmental sciences, the hydrophobicity is often used to predict the bioconcentration factor, and the adsorption coefficient [3].

The octanol-water partition coefficient, logP, is a measure of compound hydrophobicity, which in many cases correlates well with the above chemical and biological properties. ACD/Labs has created a unique additive-constitutive algorithm for the prediction of logP, based on the well-characterized logP contributions of separate atoms, structural fragments, and intramolecular interactions between different fragments.

However, the logP can be accurately calculated only for uncharged substances. If the chemical compound contains one or more ionogenic groups (i.e., functional groups which can easily form ions), it may exist as a mixture of different ionic forms. The composition of this mixture depends strongly on pH.

In such cases, the apparent partition coefficient D for dissociative systems (or logD) gives a more appropriate description of complex partitioning equilibria.

The following scheme presents an example of the complex equilibrium that exists for a solution of alanine in a water-octanol mixture:

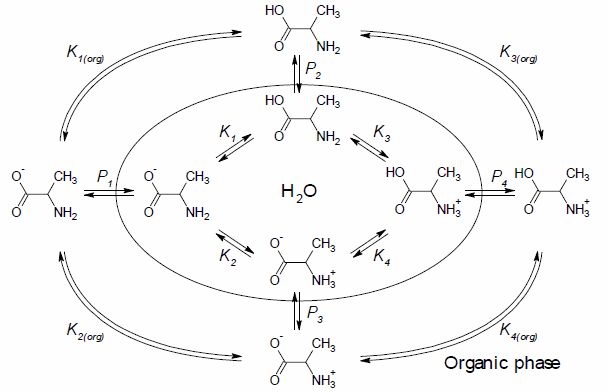
• K_i — the ionization constant of the i-th microspecies
• K_i(org) — the ionization constant of the i-th microspecies in octanol
• P_i — the partition coefficient of the i-th microspecies

So, if such complex equilibria exist, then the partitioning of chemicals between water and the organic phase should be a function of:

• the extent of ionization and
• the partition constants

of the numerous different microspecies shown in the diagram above.

These problems have already been tackled, and to a good degree of success, by two ACD/Labs algorithms:

• the acid-base ionization coefficient, pK_a, can be predicted normally to within ±0.2 pK_a units for most functional groups by ACD/pKa; and
• the octanol-water partition coefficients can be predicted normally to within ±0.3 logP units by ACD/LogP.

Thus, it only makes sense to combine the capabilities of both prediction engines in one simple-to-use prediction of logD.

Definition of LogD

The partition coefficient for dissociative mixtures, logD, is defined as follows:

logD = log(Σa_i^org / Σa_i^water)

where

• a_i^water is the concentration of i-th microspecies in water
• a_i^org is the concentration of i-th microspecies in the organic phase

For the correct solution of a proposed scheme of equilibrium, we use the master equation approach. We construct a system of equations where the concentrations of all microspecies (both in organic and aqueous phase) are represented by a set of independent linear equations.

To calculate the concentrations of all microspecies at any pH, we need to solve the following system of equations:

a_i^water = a_j^water x [H⁺] / K_i
a_i = a_i^water + a_i^org
Σa_i = 1
a_i^org = a_i^water x P_i

where

• K_i — the ionization constant of the i-th microspecies; K_i = 10^-pKa
• P_i — the partition coefficient of the i-th microspecies;
• a_j — the total concentration of the j-th microspecies having one H⁺ less than the i-th;
• a_i — the total concentration of the i-th microspecies in both H₂O and octanol.

Once the concentrations are known, the ratio Σa_i^org / Σa_i^water and thus the logD value can easily be determined.

Calculation of LogP for Microspecies

To calculate the logP of the neutral form of a given chemical structure, one of the different available ACD/LogP models (Classic, GALAS, or Consensus), that is set as a Default LogP model is used. Further details of these algorithms may be found in the ACD/LogP Technical information section.

To calculate the logP of the charged microspecies, certain empirical rules were applied. Different corrections to the logP values of the neutral form were applied, depending on the charge of the microspecies. For example, for zwitterionic forms we correct the logP of the neutral form by –2.5 because an intensive analysis showed that this correction factor led to the best fit over a wide variety of compounds.

Note that the logD calculation algorithm takes into account the partitioning of ion pairs. The formation of ion-pairs is referred to as physiological conditions, which presume an ionic strength of 0.15M. The ion-pairs are presumed to be transferred to organic phase like any non-charged form. The ionic strength is equal to the concentration of such monovalent ions as Na⁺, K⁺ (counter ions for organic anions) and Cl^– and Br^– (counter ions for organic cations).

Ionization Constants of Microspecies

To calculate the ionization constants of microspecies, the program creates a full scheme for the dissociation of a compound, and then all microconstants are calculated using one of the two available pKa prediction algorithms (Classic or GALAS) that is set as a Default pKa model in ACD/Percepta settings.

Further details of the prediction algorithm for the ionization constants of microspecies may be found in the ACD/pKa Technical information section.

References

1. Hansch, C.; Leo, A.J. Substituent constants for Correlation Analysis in Chemistry and Biology. Wiley: New York, 1979.
2. Hansch, C.; Leo, A.J. Exploring QSAR. Fundamentals and Applications in Chemistry and Biology. ACS, Washington, DC 1995.
3. Warren J. Lyman, et al. Handbook of Chemical Property Estimation Methods. ACS, Washington, DC, 1990.