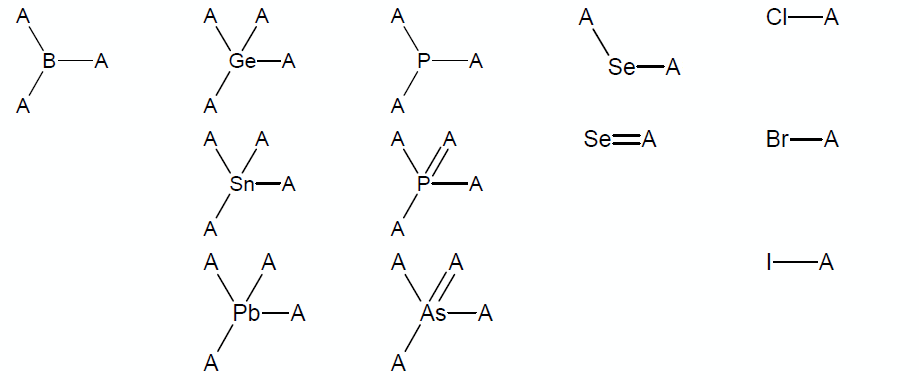LogS: Difference between revisions
No edit summary |
|||
| (3 intermediate revisions by the same user not shown) | |||
| Line 14: | Line 14: | ||
[[Image:Logs.png|center]] | [[Image:Logs.png|center]] | ||
<br /> | <br /> | ||
# Quantitative solubility (logS, | # Quantitative solubility in pure water (logS<sub>w</sub>) in selected measurement units and pH value of the resulting solution, as well as solubility in buffer (logS), estimated at various physiologically important pH values. [[File:Logs_phpoint.png|right]]<br>a. Select different measurement units.<br>b. Click "+/-" nodes to expand/collapse the option of new pH point's addition.<br>c. Enter desirable pH value and press "Add". The new pH point along with automatically calculated logS value will appear at the end of the list.<br>d. Hover over the pH point and press the "x" pictogram to remove it from the list. | ||
# Press "Configure" button to select pKa and intrinsic solubility calculation algorithms, and libraries to use for training, or set other options.<br>'''NOTE:''' Training takes place through LogS0 Self-training Libraries. The training procedure implemented in ACD/LogS0 GALAS module accepts both LogSw measured in pure water and LogS at any pH. These values are automatically recalculated to the respective LogS0 of neutral form to be stored in the library. The trained LogS0 library may then be used for LogS0, LogSw, and LogS calculations. | # Press "Configure" button to select pKa and intrinsic solubility calculation algorithms, and libraries to use for training, or set other options.<br>'''NOTE:''' Training takes place through LogS0 Self-training Libraries. The training procedure implemented in ACD/LogS0 GALAS module accepts both LogSw measured in pure water and LogS at any pH. These values are automatically recalculated to the respective LogS0 of neutral form to be stored in the library. The trained LogS0 library may then be used for LogS0, LogSw, and LogS calculations. | ||
# Graphical plot of solubility-pH dependence | # Graphical plot of solubility-pH dependence | ||
# Click and drag the slider to see calculated logS at precise pH value displayed on the right. | # Click and drag the slider to see calculated logS at precise pH value displayed on the right. | ||
<br> | <br> | ||
<div class="mw-collapsible"> | |||
==Technical information== | |||
<div class="mw-collapsible-content"> | |||
===Introduction to Aqueous Solubility=== | |||
The aqueous solubility of a chemical may be defined as the maximum amount of the chemical that will dissolve in pure water at a specified temperature. Above this concentration, two phases will exist if the organic chemical is a solid or a liquid at the system temperature: a saturated aqueous solution and a solid or liquid organic phase. | |||
'''ACD/Percepta''' predicts three types of solubility: | |||
* solubility as a function of pH (log''S''); | |||
* solubility observed when adding pure compound to unbuffered water (log''S''<sub>w</sub>); | |||
* intrinsic solubility or solubility for neutral form of compound (log''S''<sub>0</sub>). | |||
The overall solubility in buffer at given pH is a function of the intrinsic solubility of the compound and its extent of ionization at that pH. Hence, the particular setup for log''S'' predictions depends on the combination of settings for calculating log''S''<sub>0</sub> and pK<sub>a</sub>. | |||
===Algorithms for Calculating Intrinsic Solubility=== | |||
To calculate the solubility of the neutral form of a given chemical structure (log''S''<sub>0</sub>), one of the two available ACD/LogS0 models (Classic or GALAS), that is set as a '''Default LogP model''' is used. More information about ACD/LogS0 algorithm may be found in the [[ACD/LogS0_GALAS#Technical_information|ACD/LogS0 GALAS Technical information]] section. | |||
ACD/LogS0 Classic algorithm has the following features: | |||
* Compounds subdivided into classes with separate prediction equations for each, including new parameters for internal hydrogen bonds. | |||
* The following parameters are used in correlation equations: boiling point, logP/logD, MW, Molar Volume (MV), Hydrogen Bonding (number of H-acceptors and H-donors in the molecule), and refractive index. | |||
===Algorithms for Calculating the Extent of Ionization=== | |||
The ionization constants of the considered molecules are calculated using one of the two available pK<sub>a</sub> prediction algorithms (Classic or GALAS) that is set as a '''Default pKa model''' in '''ACD/Percepta''' settings. Further details of these algorithms may be found in the [[pKa#Technical_information|ACD/pKa Technical information]] section. | |||
===Limitations of ACD/Solubility Classic Algorithm=== | |||
ACD/Solubility Classic algorithm does not calculate solubility values for the following chemical structures: | |||
* Charged structures containing IV-valent Nitrogen (+), except for the non-ionic derivatives of IV-valent Nitrogen (+) bonded to Oxygen (-) or bonded to Nitrogen (-) with double bond | |||
* Structures containing atoms other than C, H, O, S, N, and F in reasonable chemical surroundings or structures containing atoms P, Cl, Br, I, Se, Si, Ge, Pb, Sn, As, or B that are not within the chemical surroundings shown below (note that A denotes any atom out of C, O, S, N, F, or any group listed below): | |||
[[File:Classic_Algorithm_Limitations.png]] | |||
* Structures that contain elements in their non-typical valence | |||
* Structures with coordinating bonds | |||
* Structures containing more than 255 atoms excluding hydrogen (note that the program refuses to predict solubility for some cyclic compounds having less than 255 atoms due to the fact that the program uses a cycle-breaking algorithm that increases the number of atoms). | |||
'''Note:''' The groups from the table except sp<sup>3</sup>-hybridized selene cannot be a part of a cycle. | |||
The program does not take into account the specific features of different geometric isomers, stereoisomers, conformers, isotopes, and structures with non-covalent bonds. | |||
It predicts solubility values so that in most cases the reliable experimental measurements lie within the following solubility interval: 0.2–0.5 units for simple compounds and 0.5–1.0 units for complex compounds. However, it is still possible that some new chemical structures might possess new specific structural features, such as far-range non-covalent bonding, intra-molecular shielding, or inter-molecular association. In such cases, the discrepancy between a newly measured experimental value and the calculated solubility interval might occur. | |||
'''Note:''' There certainly exist some structures that formally meet the aforementioned limitations, but cannot be calculated by the current algorithm. | |||
</div> | |||
</div> | |||
Latest revision as of 08:48, 8 August 2018
Overview
LogS module simulates the full solubility-pH profile. Prediction results are presented in two ways – an easy to navigate and interpret graph and a list of LogS predictions at discrete pH values. Initially this list is populated by the solubility predictions at physiologically relevant pH conditions; however it is fully customizable via the ability to add or remove the predictions at any pH value.
Features
- Estimates the solubility in pure water and pH value of the resulting solution
- Estimates the solubility-pH profile and calculates LogS values at various physiological pHs
Interface
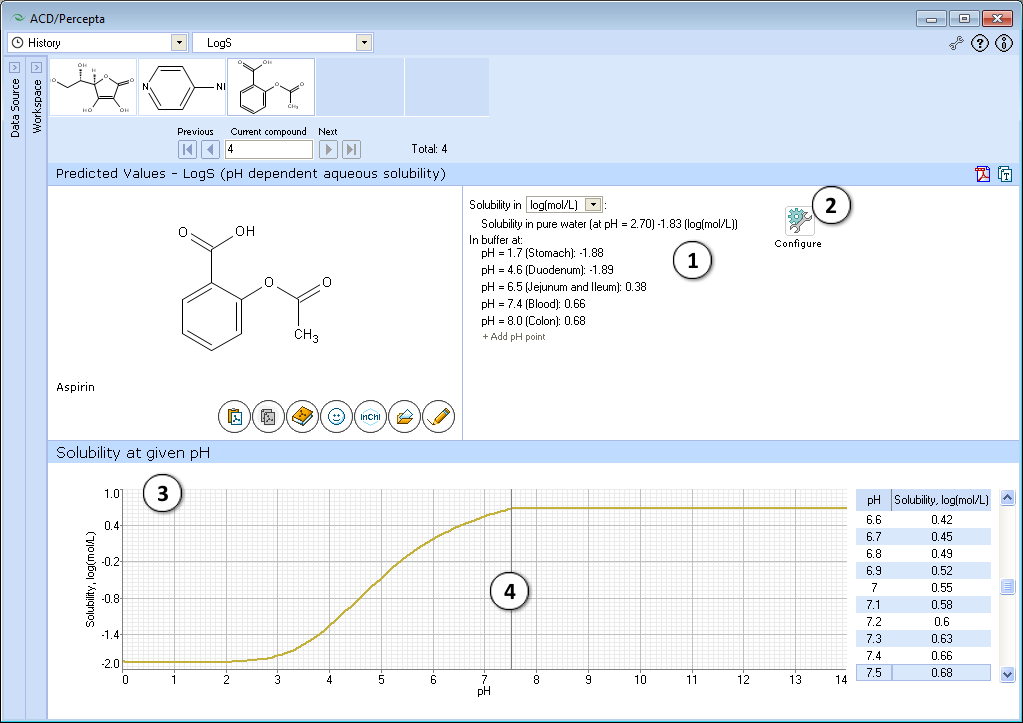
- Quantitative solubility in pure water (logSw) in selected measurement units and pH value of the resulting solution, as well as solubility in buffer (logS), estimated at various physiologically important pH values.

a. Select different measurement units.
b. Click "+/-" nodes to expand/collapse the option of new pH point's addition.
c. Enter desirable pH value and press "Add". The new pH point along with automatically calculated logS value will appear at the end of the list.
d. Hover over the pH point and press the "x" pictogram to remove it from the list. - Press "Configure" button to select pKa and intrinsic solubility calculation algorithms, and libraries to use for training, or set other options.
NOTE: Training takes place through LogS0 Self-training Libraries. The training procedure implemented in ACD/LogS0 GALAS module accepts both LogSw measured in pure water and LogS at any pH. These values are automatically recalculated to the respective LogS0 of neutral form to be stored in the library. The trained LogS0 library may then be used for LogS0, LogSw, and LogS calculations. - Graphical plot of solubility-pH dependence
- Click and drag the slider to see calculated logS at precise pH value displayed on the right.
Technical information
Introduction to Aqueous Solubility
The aqueous solubility of a chemical may be defined as the maximum amount of the chemical that will dissolve in pure water at a specified temperature. Above this concentration, two phases will exist if the organic chemical is a solid or a liquid at the system temperature: a saturated aqueous solution and a solid or liquid organic phase.
ACD/Percepta predicts three types of solubility:
- solubility as a function of pH (logS);
- solubility observed when adding pure compound to unbuffered water (logSw);
- intrinsic solubility or solubility for neutral form of compound (logS0).
The overall solubility in buffer at given pH is a function of the intrinsic solubility of the compound and its extent of ionization at that pH. Hence, the particular setup for logS predictions depends on the combination of settings for calculating logS0 and pKa.
Algorithms for Calculating Intrinsic Solubility
To calculate the solubility of the neutral form of a given chemical structure (logS0), one of the two available ACD/LogS0 models (Classic or GALAS), that is set as a Default LogP model is used. More information about ACD/LogS0 algorithm may be found in the ACD/LogS0 GALAS Technical information section.
ACD/LogS0 Classic algorithm has the following features:
- Compounds subdivided into classes with separate prediction equations for each, including new parameters for internal hydrogen bonds.
- The following parameters are used in correlation equations: boiling point, logP/logD, MW, Molar Volume (MV), Hydrogen Bonding (number of H-acceptors and H-donors in the molecule), and refractive index.
Algorithms for Calculating the Extent of Ionization
The ionization constants of the considered molecules are calculated using one of the two available pKa prediction algorithms (Classic or GALAS) that is set as a Default pKa model in ACD/Percepta settings. Further details of these algorithms may be found in the ACD/pKa Technical information section.
Limitations of ACD/Solubility Classic Algorithm
ACD/Solubility Classic algorithm does not calculate solubility values for the following chemical structures:
- Charged structures containing IV-valent Nitrogen (+), except for the non-ionic derivatives of IV-valent Nitrogen (+) bonded to Oxygen (-) or bonded to Nitrogen (-) with double bond
- Structures containing atoms other than C, H, O, S, N, and F in reasonable chemical surroundings or structures containing atoms P, Cl, Br, I, Se, Si, Ge, Pb, Sn, As, or B that are not within the chemical surroundings shown below (note that A denotes any atom out of C, O, S, N, F, or any group listed below):
- Structures that contain elements in their non-typical valence
- Structures with coordinating bonds
- Structures containing more than 255 atoms excluding hydrogen (note that the program refuses to predict solubility for some cyclic compounds having less than 255 atoms due to the fact that the program uses a cycle-breaking algorithm that increases the number of atoms).
Note: The groups from the table except sp3-hybridized selene cannot be a part of a cycle.
The program does not take into account the specific features of different geometric isomers, stereoisomers, conformers, isotopes, and structures with non-covalent bonds.
It predicts solubility values so that in most cases the reliable experimental measurements lie within the following solubility interval: 0.2–0.5 units for simple compounds and 0.5–1.0 units for complex compounds. However, it is still possible that some new chemical structures might possess new specific structural features, such as far-range non-covalent bonding, intra-molecular shielding, or inter-molecular association. In such cases, the discrepancy between a newly measured experimental value and the calculated solubility interval might occur.
Note: There certainly exist some structures that formally meet the aforementioned limitations, but cannot be calculated by the current algorithm.